Chance and Chaos (FFR 150)
(4.5 credit units)
Bernhard Mehlig (lectures, examiner) Office: S3050
Schedule
The course consists of seven 2h lectures introducing the mathematical methods and computational tools.
Plan
Stochastic dynamics in Physics, Chemistry, and Biology. The course provides an introduction to stochastic models of complex systems. What are complex systems? Many systems observed in the world around us exhibit apparently irregular fluctuations. Examples are the density variations of inertial particles moving in random flows (Fig. 1), cross-section fluctuations in the photodissociation of large molecules, but also the apparently random patterns of genetic variation in the human genome (Fig. 2). The cause of the apparently random fluctuations is the same in all cases: irregular dynamics. It may be a consequence of disorder (due to randomly distributed impurities for example), it may arise dynamically (as in chaotic motion in highly excited molecules), it may be due to the interaction of a large (but finite) number of individuals (as in the evolution of the human genome), or may be a consequence of the interaction of many constituents (gas molecules forming a turbulent fluid). These examples have in common that the number of degrees of freedom exceeds the number of conservation laws. This makes the corresponding systems complex, and requires stochastic methods to describe the empirically observed fluctuations.
Literature
1. B. Mehlig, Chaos and Disorder: Dynamics of Complex Systems, Lecture notes, Freiburg (1999)
2. N. G. van Kampen, Stochastic processes in physics and chemistry, 2nd edition, North-Holland (1992)
3. O. Bohigas, Random matrices and chaotic dynamics, in: Chaos and Quantum Physics, eds: G. J. Giannoni, A. Voros and J. Zinn-Justin, North-Holland (1991)
4. Lecture notes for this course
Examination
Credits for this course are obtained by solving the homework set (solutions of examples and programming projects). There are two sets of homework which are graded.
Every student must hand in her/his own solution on paper. Same rules as for written exams apply: it is not allowed to copy any material from anywhere unless appropriate reference is given. All figures must have axis labels and captions giving all information necessary to reproduce the figure. Describe your results in words. Always compare with theory. Summarise problems, discuss possible reasons. Program code must be appended. Each of the five examples sheet gives 5 points. In order to pass the course at least 14 points are required. The examples sheets will be processed by URKUND. Your solutions should be submitted before the deadline as PDF files electronically to
Examples

Fig. 1: Distribution of inertial particles suspended in a randomly moving gas. Blue corresponds to low, yellow to high particle density. The figure illustrates a striking similarity with optical patterns that can be seen at the bottom of a swimming pool on a sunny day [M. Berry, Nature 267, 34-36 (1977)].
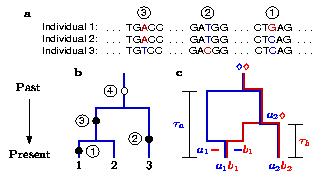
Fig. 2: a In DNA, genetic information is encoded by the sequence of the four nucleic acids adenine (A), thymine (T), guanine (G), and cytosine (C). In a sample of three individuals, three polymorphic sites are shown. b The most common variation is a difference at a single position (single-nucleotide polymorphism or SNP), caused by a mutation at one position. The three mutations in panel a are shown as filled circles in a genealogy of the three individuals (blue). Mutation 4 does not cause a polymorphism in the sample, since all individuals in the sample inherit the mutation from the common ancestor. c In recombination, one of the two copies of a chromosome is inherited from one parent and the rest from the other parent. A sample gene history with one recombination event is shown, for two loci (a and b).