Turbulent aerosols

Turbulent aerosols are suspensions of heavy particles in a turbulent fluid. Examples  are micron-sized water droplets or small ice crystals in turbulent clouds, virus-carrying droplets in the turbulent jet of exhaled air, or micron-sized dust grains in the turbulent gas around a growing star -- grain aggregation is thought to be the first stage of planet formation.

How do the particles grow or shrink in size by collisional aggregation or fragmentation,  and in the case of droplets, by condensation or evaporation? Turbulence plays an essential role -- it may accelerate or slow down particle growth -- but the mechanisms are not understood because  the analysis of these highly non-linear and multi-scale systems poses formidable challenges. Experiments resolving the motion of tiny particles in turbulence have only recently become possible, and direct numerical simulation of such systems is still immensely difficult.

Therefore we pursue a different approach: we derive idealised statistical models for turbulent aerosols that can be rigorously analysed using methods from non-equilibrium statistical physics and dynamical-systems theory. The turbulent velocity fluctuations are represented in terms of a stochastic synthetic turbulence model, and perturbation theory makes it possible to compute how  the particles sample the turbulence, assuming that they do not directly interact. This allowed us to  identify and describe key mechanisms that determine fractal spatial patterns of particles in dilute turbulent aerosols (Figure 1). See our review article [1] for a summary of recent progress.

Ref. [2] reviews how to compute Lyapunov exponents and fractal dimensions to characterise these patterns, using WKB methods and resummed high-order perturbation theory. The perturbation coefficients are integers (Table 1) or rational numbers with small denominators. The integer coefficients occur in other problems too, indicating underlying connections with these problems (for instance numbers and weights of Feynman diagrams, Wiener index of random trees, Brownian bridges). See series A062980 in the on-line encyclopedia of integer sequences.

A striking example is the formation of singularities in the particle dynamics analogous to caustic patterns formed by sun light at the bottom of a swimming pool. This is an inertial effect. As the particle detach from the fluid flow, their phase-space manifolds fold over (Figure 2), resulting in caustic patterns and large relative velocities between nearby particles. Settling changes the particle paths, it tends to slow down caustic formation [5].

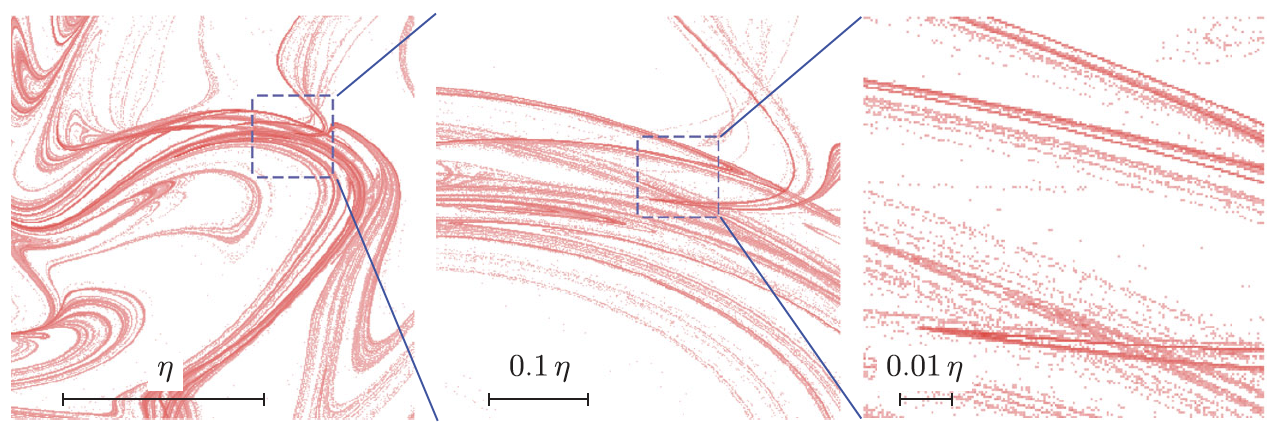
Figure 1. Fractal spatial patterns observed in statistical-model simulations of a turbulent aerosol. From Ref. [2].

 

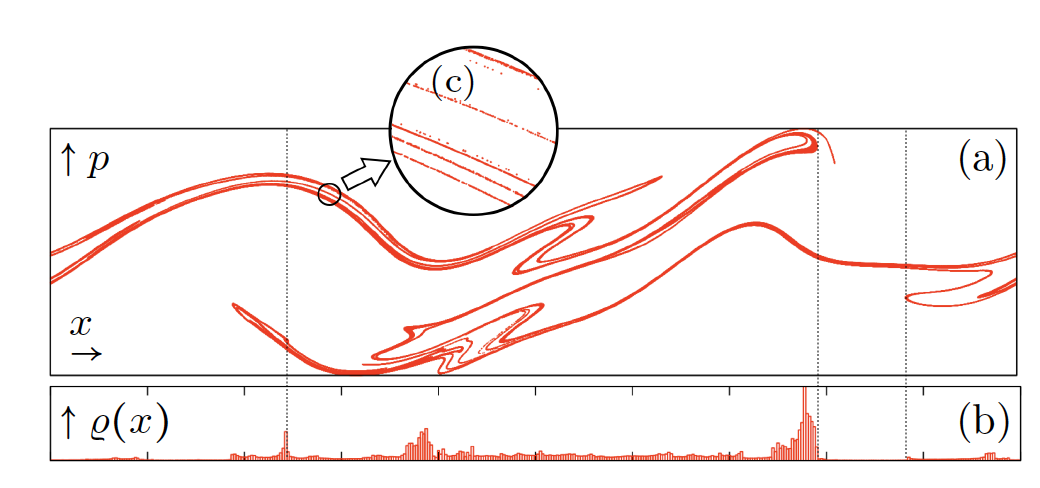
Figure 2. (a) Snapshot of a fractal attractor in phase space (particle position x, particle momentum p) for a one-dimensional statistical model. Folds of the attractor correspond to caustics [3]. (b) Particle-number density fluctuations due to caustics. (c) The inset illustrates that the attractor is fractal. From Ref. [4].

Table 1. First 10 coefficients of the perturbation expansion for the maximal Lyapunov exponent describing how spatial separations between nearby particles change (one-dimensional statistical model, white-noise limit). See Figure 14 in Ref. [2] and series A062980 in the on-line encyclopedia of integer sequences.

[1] Statistical models for the dynamics of heavy particles in turbulence
J. Bec, K. Gustavsson, B. Mehlig, Annu. Rev. Fluid Mech. (2024)
 DOI: 2010.1146/annurev-fluid-032822-014140

[2] Statistical models for spatial patterns of heavy particles in turbulence
K Gustavsson, B Mehlig, Advances in Physics 65 (2016) 1-57

[3] Caustics in turbulent aerosols
M Wilkinson & B Mehlig, Europhysics Letters 71 (2005) 186

[4] Fractal catastrophes
J Meibohm, K Gustavsson, J Bec & B Mehlig, New Journal of Physics 22 (2020), 013033

[5] Clustering of particles falling in a turbulent flow
K Gustavsson, S Vajedi & B Mehlig, Physical Review Letters 112 (2014), 214501