Staggered-ladder spectra

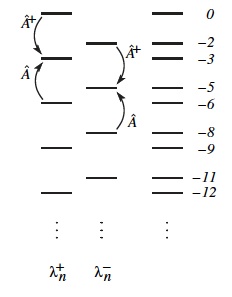There are only few physically significant systems with exactly evenly spaced energy levels. Examples are the harmonic oscillator and the Zeeman-splitting Hamiltonian. In Refs. [1,2] we solved a family of eigenvalue problems that occur in an extension of a classic problem in the theory of diffusion, the stochastic Ornstein-Uhlenbeck process. Our system is also closely related to a model for stochastic acceleration, introduced by Sturrock to describe the acceleration of charged particles by interstellar fields. Golubovic et al. and Rosenbluth found that the model may exhibit superdiffusion of the particles.

Our eigenvalue problems have ladder spectra, but they differ from the usual examples in that their spectra consist of two ladders which are staggered; the eigenvalues for eigenfunctions of odd and even symmetry do not interleave with equal spacings. To solve the problem, we introduce a new type of raising and lowering operators, which are nonlinear second-order differential operators. Our solution yields an exact expression for the superdiffusion law, and it predicts a non-Gaussian distribution of the particle momentum in the steady state.

The model was extended by [Y. Krivolapov et al., New. J. Physics (2012)] and  [L. Levi et al., Nature Physics (2012)] to explain the experimental observation of superdiffusion of light in a disordered medium.

[1] Staggered Ladder Spectra
E Arvedson, M Wilkinson, B Mehlig & K Nakamura, Physical Review Letters 96 (2016) 030601

[2] Generalized Ornstein-Uhlenbeck Processes
V Bezuglyy, B Mehlig, M Wilkinson, K Nakamura, & E Arvedson, Journal of Mathematical Physics 47 (2016), 073301